Lambert-Beersches-Gesetz

Formel

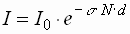
I	:	Intensität des Lichtstrahls nach Durchlaufen der Lösung
I0	:	Intensität des Lichtstrahls vor Durchlaufen der Lösung
s	:	konzentrationsunabhängiger Absorptionsquerschnitt
N	:	Teilchenkonzentration
d	:	Schichtdicke

Herleitung

• Schickt man Licht durch ein absorbierendes Medium, so nimmt seine Intensität dabei exponentiell ab. Es gilt das Lambertsche Gesetz:

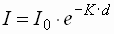
I	:	Intensität nach Durchlaufen der Probe
I0	:	ursprüngliche Intensität
K	:	stoffspezifischer Absorptionskoeffizient, im allgemeinen abhängig von der Wellenlänge
d	:	Schichtdicke der Probe

• Das Beersche Gesetz hat folgende Form:

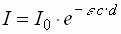
I	:	Intensität nach Durchlaufen der Probe
I0	:	ursprüngliche Intensität
e	:	molarer Extinktionskoeffizient
c	:	molare Konzentration
d	:	Schichtdicke der Probe

• Damit hat es die gleiche formale Gestalt, wie das Lambertsche Gesetz. Es behauptet jedoch über dieses hinaus, dass der gemessene Wert der Absorption einer absorbierenden Substanz in einem nicht absorbierenden Medium immer dann gleich ist, wenn die molare Konzentration c sich umgekehrt wie die Schichtdicke d verhält. 
• Für Lösungen absorbierender Stoffe in einem nicht absorbierenden Medium gilt das Beersche Gesetz ausgezeichnet. Abweichungen treten lediglich bei hohen Konzentrationen auf. Abweichungen ergeben sich außerdem bei Festkörpern, insbesondere Halbleitern.
• Im Lambert-Beerschen-Gesetz sind die oben vorgestellten Gesetze miteinander verknüpft. Dazu kommt die atomistische Deutung, dass den "Teilchen" des gelösten absorbierenden Stoffes ein konzentrationsunabhängiger Absorptionsquerschnitt s zukommt.
• Damit lässt sich der stoffspezifische Absorptionskoeffizient K darstellen als:

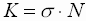
K	:	stoffspezifischer Absorptionskoeffizient
s	:	Absorptionsquerschnitt
N	:	Teilchenkonzentration

• Für das Lambert-Beersche-Gesetz ergibt sich somit die oben dargestellte Formel.

Anwendung

• In der Pharmazie findet das Lambert-Beersche-Gesetz bei der Messung der Absorption bestimmter Stoffe und deren Konzentrationen Anwendung. Dazu wird eine umgeformte Version des Gesetzes benutzt.
• Die Absorption einer Lösung lässt sich wie folgt berechnen:

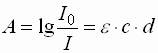
A	:	Absorption
I0	:	Ausgangsintensität des Lichtstrahls
I	:	Intensität des Lichtstrahls nach Durchlaufen der Probe
e	:	molarer Extinktionskoeffizient
c	:	molare Konzentration
d	:	Schichtdicke

Anwendbarkeit / Bedingungen 

• Verwendung monochromatischen Lichts
• Konzentration der Lösungen kleiner 10^-2 mol/l, da oberhalb dieses Wertes die optischen Eigenschaften, aufgrund von Wechselwirkungen der Moleküle untereinander, etwas geändert sind.
• Verwendung des gleichen Lösemittels, wie in der Literaturangabe des verwendeten e.